Il moto circolare uniforme in coordinate cartesiane
Il moto circolare uniforme può essere descritto utilizzando la coordinata angolare \( \theta \) e introducendo la velocità angolare \( \omega \), come abbiamo fatto qui.
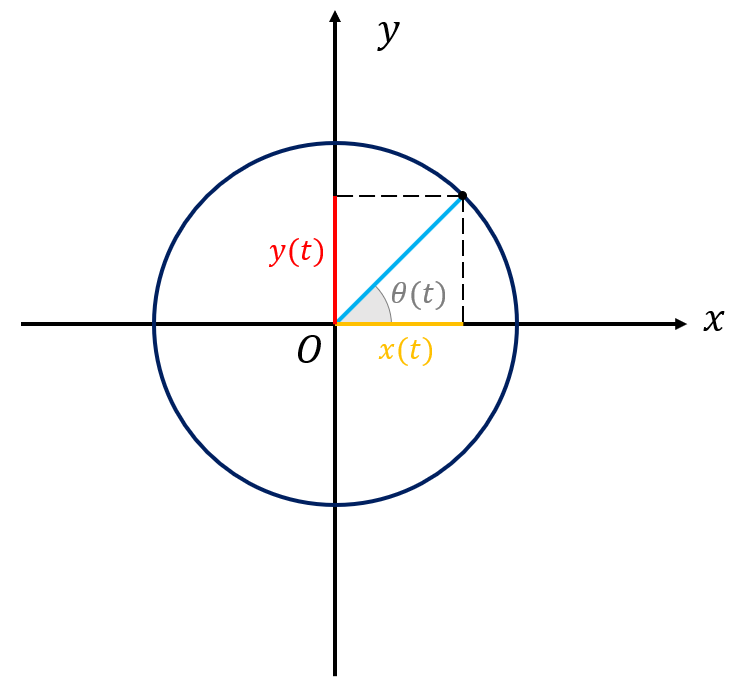
Possiamo però anche descrivere il moto circolare utilizzando le coordinate cartesiane \( x \) e \( y \). Esse sono legata alla coordinata angolare \( \theta \) dalle relazioni trigonometriche:
$$\begin{cases} x(t) = R \cos \left ( \theta(t) \right ) \\ y(t) = R \sin \left ( \theta(t) \right ) \end{cases}$$
dove \( R \) è il raggio della circonferenza e abbiamo esplicitato la dipendenza temporale delle grandezze cinematiche.
Poiché, per definizione, nel moto circolare uniforme la velocità angolare \( \omega = \frac{d\theta}{d t} \) è costante, la coordinata angolare \( \theta \) varia secondo la legge lineare
$$\theta (t) = \theta _0 + \omega (t-t_0)$$
Possiamo, per semplicità, fissare l’istante iniziale \(t_0 = 0 \) e l’angolo iniziale \( \theta(t=0) = \theta_0 = 0\), quindi la precedente legge si semplifica in
$$\theta (t) = \omega t$$
Da cui le leggi orarie scritte per le coordinate cartesiane diventano:
$$\begin{cases} x(t) = R \cos \left ( \theta(t) \right ) \\ y(t) = R \sin \left ( \theta(t) \right ) \end{cases}$$
Equazione della traiettoria
Per determinare l’equazione della traiettoria, eleviamo al quadrato le due leggi orarie:
$$\begin{cases} x^2= R^2 \cos^2 \left ( \omega t \right ) \\ y^2 = R^2 \sin^2 \left ( \omega t \right ) \end{cases}$$
Ora sommiamo membro a membro queste due equazioni:
$$x^2 + y^2 = R^2 \cos^2 \left ( \omega t \right ) + R^2 \sin^2 \left ( \omega t \right )$$
$$x^2 + y^2 = R^2 \left [ \cos^2 \left ( \omega t \right ) + \sin^2 \left ( \omega t \right ) \right ]$$
E ricordando l’identità goniometrica \( \cos^2 \left ( x \right ) + \sin^2 \left ( x \right ) = 1 \) otteniamo:
$$x^2 + y^2 = R^2 $$
che è proprio l’equazione di una circonferenza di raggio \( R \), come deve essere per un moto circolare.
Velocità
Calcoliamo le due componenti del vettore velocità \( \vec{v} = (v_x , v_y)\):
$$\begin{cases} v_x(t) = \frac{dx}{dt} = \frac{d}{dt} [R \cos \left ( \omega t \right )] = – \omega R \sin \left ( \omega t \right ) \\ v_y(t) = \frac{dy}{dt} = \frac{d}{dt} [R \sin\left ( \omega t \right )] = \omega R \cos \left ( \omega t \right ) \end{cases}$$
Possiamo riconoscere le due coordinate cartesiane \( x(t) = R \cos \left ( \omega t \right ) \) e \( y(t) = R \sin \left ( \omega t \right ) \). Quindi riscriviamo le componenti della velocità:
$$\begin{cases} v_x(t) = – \omega y(t) \\ v_y(t) = \omega x(t) \end{cases}$$
Il modulo quadro del vettore velocità è:
$$\begin{aligned} \left | \vec{v} \right |^2 &= v_x^2 + v_y^2 = \omega^2 R^2 \sin^2 \left ( \omega t \right ) + \omega^2 R^2 \cos^2 \left ( \omega t \right ) \\ &= \omega^2 R^2 \left [ \sin^2 \left ( \omega t \right ) + \cos^2 \left ( \omega t \right ) \right ] \\ &= \omega^2 R^2 \end{aligned}$$
Quindi il modulo del vettore velocità è:
$$\left | \vec{v} \right | = \omega R $$
Accelerazione
Calcoliamo le due componenti del vettore accelerazione \( \vec{a} = (a_x , a_y)\):
$$\begin{cases} a_x(t) = \frac{d v_x}{dt} = \frac{d}{dt} [- \omega R \sin \left ( \omega t \right )] = – \omega^2 R \cos \left ( \omega t \right ) \\ a_y(t) = \frac{d v_y}{dt} = \frac{d}{dt} [\omega R \cos \left ( \omega t \right )] = – \omega^2 R \sin \left ( \omega t \right ) \end{cases}$$
Possiamo riconoscere le due coordinate cartesiane \( x(t) = R \cos \left ( \omega t \right ) \) e \( y(t) = R \sin \left ( \omega t \right ) \). Quindi riscriviamo le componenti della accelerazione:
$$\begin{cases} a_x(t) = – \omega^2 x(t) \\ a_y(t) = \omega^2 y(t) \end{cases}$$