Spostamento, velocità, accelerazione

Consideriamo una particella che si muove nello spazio. In figura abbiamo indicato con \(\gamma\)  la sua traiettoria, ovvero il luogo di punti per cui è passata la particella.

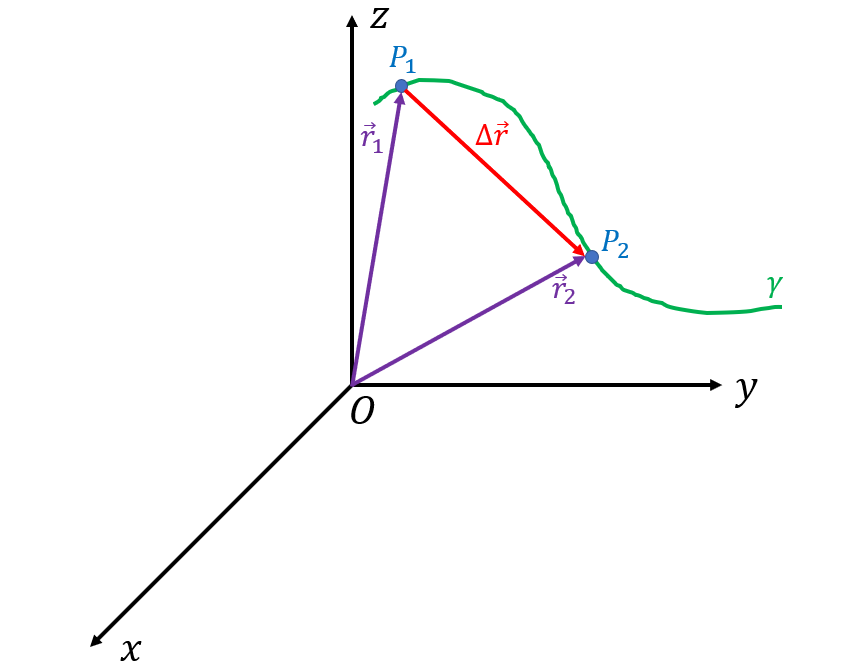
Spostamento

Indichiamo con \( \vec{r} \) il vettore che individua la posizione della particella. In generale, poiché la posizione della particella varia nel tempo, avremo a che fare con una funzione \( \vec{r} (t) \) , che viene chiamata legge oraria. In altre parole, la legge oraria è la funzione che descrive la posizione di una particella al variare del tempo.

Dato che \( \vec{r} (t) \) è un vettore, equivale a $$ \vec{r} (t) = \begin{cases} x(t) \\ y(t) \\ z(t) \end{cases} $$

che possiamo anche scrivere con la seguente notazione:

$$ \vec{r} = \left( x(t) , y(t) , z(t) \right )$$

Supponiamo che la particella si trovi nel punto \( P_1 \) all’istante di tempo \( t \) e nel punto \( P_2 \) ad un istante di tempo successivo, \( t + \Delta t \) .

Possiamo quindi descrivere le due posizioni della particella mediante i vettori

• \( \vec{r}_1 = \vec{r} (t) \)
• \( \vec{r}_2 = \vec{r} (t + \Delta t ) \)

Per definizione, il vettore spostamento è la differenza di questi due vettori: $$\Delta \vec{r} = \vec{r}_2 – \vec{r}_1 $$

Velocità media e velocità istantanea

Definiamo la velocità media della particella in un intervallo di tempo finito \( \Delta t \) come il rapporto tra il vettore spostamento e l’intervallo di tempo considerato:

$$ \vec{v}_m = \frac{ \Delta \vec{r} }{\Delta t} $$

La velocità media è un vettore, avente stessa direzione e stesso verso del vettore spostamento. Esplicitandone le tre componenti cartesiane:

$$ \vec{v}_m = \begin{cases} \frac{\Delta x}{\Delta t} \\ \frac{\Delta y}{\Delta t} \\ \frac{\Delta z}{\Delta t} \end{cases}$$

oppure:

$$ \vec{v}_m = \left( \frac{\Delta x}{\Delta t} , \frac{\Delta y}{\Delta t} , \frac{\Delta z}{\Delta t} \right )$$

L’unità di misura della velocità media nel Sistema Internazionale è il metro al secondo, in simboli m/s.

La velocità media in genere varia al variare dell’intervallo di tempo \( \Delta t \) considerato.

Se l’intervallo di tempo \( \Delta t \) è “molto piccolo” possiamo immaginare che la velocità media sia costante. In questo caso parliamo di velocità istantanea.  Matematicamente dobbiamo introdurre il concetto di limite:

$$\vec{v} = \lim_{t \to 0} \frac{\Delta \vec{r}}{\Delta t}$$

Dall’analisi matematica sappiamo che il membro di destra della precedente equazione (limite di un rapporto incrementale) non è altro che la definizione di derivata.

La velocità istantanea è quindi la derivata (prima) rispetto al tempo del vettore spostamento:

$$\vec{v} = \frac{d \vec{r}}{d t}$$

Esplicitando le componenti cartesiane:

$$\vec{v} = \left ( \frac{d x}{d t} , \frac{d y}{d t} , \frac{d z}{d t} \right )$$

Accelerazione media e accelerazione istantanea

Durante il moto di un corpo, la velocità può variare in (direzione e/o modulo). Per rendere conto di queste variazioni, introduciamo la definizione di accelerazione media:

$$ \vec{a}_m = \frac{ \Delta \vec{v} }{\Delta t} $$

dove \( \Delta \vec{v} \) è la variazione di velocità avvenuta nell’intervallo di tempo finito \( \Delta t \) .

Nel Sistema Internazionale l’unità di misura dell’accelerazione è il metro al secondo quadrato, in simboli m/s². 

Analogamente a quanto discusso per la velocità, se l’intervallo di tempo \( \Delta t \) è “molto piccolo” possiamo parlare di accelerazione istantanea. 

Utilizziamo il concetto di limite per dare la definizione di accelerazione istantanea:

$$\vec{a} = \lim_{t \to 0} \frac{\Delta \vec{v}}{\Delta t}$$

Anche in questo caso, ricordiamo che il limite di un rapporto incrementale (membro di destra della precedente equazione) è per definizione una derivata. 

Quindi l’accelerazione istantanea è la derivata (prima) rispetto al tempo del vettore velocità:

$$\vec{a} = \frac{d \vec{v}}{d t}$$

Esplicitando le componenti cartesiane:

$$\vec{a} = \left ( \frac{d v_x}{d t} , \frac{d v_y}{d t} , \frac{d v_z}{d t} \right )$$

Poiché l’accelerazione istantanea è la derivata prima della velocità e, a sua volta, la velocità è la derivata prima del vettore spostamento, l’accelerazione è la derivata seconda del vettore spostamento:

$$\vec{a} = \frac{d \vec{v}}{d t} = \frac{d }{d t} \left ( \frac{d \vec{r}}{d t} \right ) = \frac{d^2 \vec{r}}{d t^2} $$